Delta Hedging

To show how Delta Hedging can be done with MesoSim, let’s consider a structure consisting of two legs (separate option contracts):

- 1 Call Option sold at around 160 DTE with the Strike closest to 10 delta.
This leg will be referred to as short_call.

- 1 Put Option sold at the same expiration as the call with the Strike selected to bring the whole structure (Short Call and Short Put together) closest to 0 delta. Practically that delta will also be around 10, but we’ve chosen to do this calculation dynamically.
This leg will be referred to as short_put. See the specific Delta reference in row 30: "Delta": "leg_short_call_delta * -1".

"Structure": {
"Name": "ShortStrangle",
"Expirations": [
   {
     "Name": "160dte",
     "DTE": "160",
     "Min": 140,
     "Max": 190
   }
],
"Legs": [
   {
     "Name": "short_call",
     "Qty": "-1",
     "ExpirationName": "160dte",
     "StrikeSelector": {
      "Min": 5,
       "Max": 15,
       "Delta": "10"
     },
     "OptionType": "Call"
   },
   {
     "Name": "short_put",
     "Qty": "-1",
     "ExpirationName": "160dte",
     "StrikeSelector": {
      "Min": 5,
       "Max": 15,
       "Delta": "leg_short_call_delta * -1"
     },
     "OptionType": "Put"
   }
]
  }

The delta selector for the short_put leg uses the previously defined short_call leg’s delta. The resulting structure’s overall delta will be around 0.

The above approach is easy to understand and works, but there is a better, more scalable way of doing it.

To illustrate, let’s consider a three-legged structure:

Broken Wing Butterfly

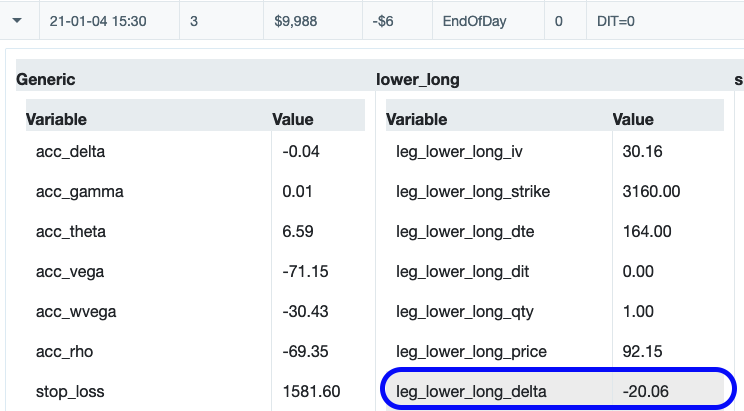
See the specific Delta reference in row 25: "Delta": "pos_delta".

"Legs": [
   {
     "Name": "upper_long",
     "Qty": "1",
     "ExpirationName": "160dte",
     "StrikeSelector": {
       "Delta": "40"
     },
     "OptionType": "Put"
   },
   {
     "Name": "short",
     "Qty": "-2",
     "ExpirationName": "160dte",
     "StrikeSelector": {
       "Delta": "30"
     },
     "OptionType": "Put"
   },
   {
     "Name": "lower_long",
     "Qty": "1",
     "ExpirationName": "160dte",
     "StrikeSelector": {
       "Delta": "pos_delta"
     },
     "OptionType": "Put"
   }]

In the above example, the last leg’s (lower_long) delta is specified using a statement that is calculated based on the overall position delta so far. At the time of the statement evaluation, two legs are already considered, and pos_delta represents their sum:

pos_delta = [ leg_upper_long_delta ] + [ leg_short_delta ]
= [1 x (-40)] + [-2 x (-30)]
= -40 + 60
= 20

If we take this delta value (which should be around: (2*30)-40=20) and choose the last (lower_long) leg using this delta value then we will end up at a delta neutral position at initiation: